Data embedding is a traditional problem in many areas from rigorous mathematics to machine learning and data mining. The problem comes from the usual practice of dimensionality reduction, that is, to project high dimensional data into a low space so that the resulting low dimensional configuration reflects intrinsic structure of the data and performs better in future processing. Traditional linear approaches such as principal component analysis (PCA) and linear discriminant analysis (LDA) are special cases of data embedding.
Data embedding has been extensively studied with many algorithms proposed. In summary, these algorithms work by taking one or both of the following two ideas:
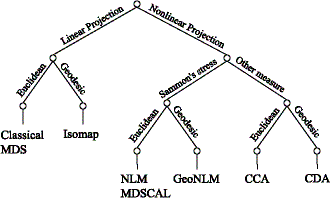
We have conducted experiments on existing distance-based embedding methods (methods using the first idea). Some of them are systematized in the figure below. We found that, among the factors used in various methods, the use of geodesic distances (estimated as lengths of shortest paths on a neighborhood graph constructed using the second idea) offers the greatest improvement to the embedding results.

Our research on data embedding has focused on the following three topics:
Data embedding approach using the second idea starts by defining neighbor points of each data point. It requires that the closure of neighbor points of each data point covers all data points. Otherwise, the approach would fail in deriving global information. If we use every data point as a vertex and connect every point to each of its neigbors by an edge, we obtain a neighborhood graph of all data points. The neighborhood graph must be a connected graph.
Neighborhood graph construction is a key step for the success of data embedding algorithms using the second idea. For example, Isomap requires a connected neighborhood graph so that the geodesic distance between any pair of data points could be estimated by the length of the shortest path between the pair. However, neither the k-NN approach (k-nearest neighbor) nor the epsilon-neighbor approach (all points within the distance epsilon) guarantees the connectedness of the constructed neighborhood graph. We have proposed four approaches, k-MST, Min-k-ST, k-EC, and k-VC, to construct connected neighborhood graphs. k-MST, Min-k-ST, and k-EC construct k-edge-connected neighborhood graphs and k-VC constructs k-connected neighborhood graphs. k-MST works by repeatedly extracting minimum spanning trees (MSTs) from the complete Euclidean graph of all data points. The rest three approaches use greedy algorithms. Each of them starts by sorting all edges in non-decreasing order of edge length. Min-k-ST works by finding k edge-disjoint spanning trees the sum of whose total lengths is a minimum. k-EC works by repeatedly adding each edge in non-decreasing order of edge length to a partially formed neighborhood graph if end vertices of the edge are not yet k-edge-connected on the graph. k-VC works in a similar way as k-EC. However, it adds an edge to a partially formed neighborhood graph if two end vertices of the edge are not yet k-connected on the graph. Experiments show that these approachs outperform the k-NN and the epsilon-neighbor approachs, especially when the input data is undersampled or unevenly distributed where the two conventional approachs would fail. The following figures illustrate an example data set and its 2D projections using Isomap with neighborhood graphs constructed by using the above approaches. Shortest paths between example pairs of points are shown to demonstrate how geodesic distances are estimated on each neighborhood graph.

(a) A Swiss-roll data set of 1,000 points superimposed with a 5-NN neighborhood graph.

(b) Data set unwarpped with the 5-NN neighborhood graph.
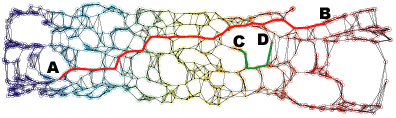
(c) 2D projection using Isomap with the 5-NN neighborhood graph.
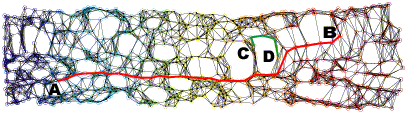
(d) 2D projection using Isomap with a 5-MST neighborhood graph.
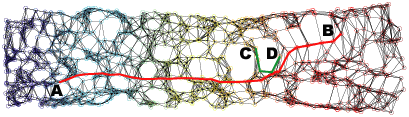
(e) 2D projection using Isomap with a Min-5-ST neighborhood graph.
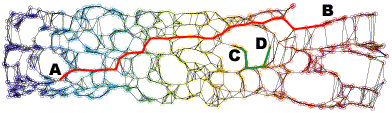
(f) 2D projection using Isomap with a 5-EC neighborhood graph.
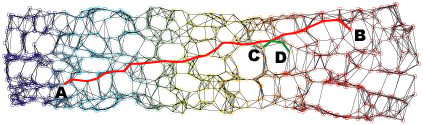
(g) 2D projection using Isomap with a 5-VC neighborhood graph.
A p-dimensional manifold locally resembles a p-dimensional Euclidean space. Therefore, data observations that lie on a manifold can be approximated by a collection of overlapping local patches, the alignment of which in a low dimensional Euclidean space would provide an embedding of the data. This idea suggests a data embedding method using classical multidimensional scaling or principal component analysis as local model. Our algorithm works by first identifying a minimum set of overlapping neighborhoods that cover all data points. This is done by applying a greedy approximation algorithm of minimum set cover. Classical multidimensional scaling is then applied to each neighborhood to derive a low dimensional patch. Overlapping local patches are finally aligned to derive the final data embedding result in order to minimize a residual measure. The residual measure has a quadratic form in terms of the resulting global coordinates and therefore can be minimized by using an eigensolver. We call this method locally multidimensional scaling (LMDS).
The overall idea of LMDS resembles that of locally linear embedding (LLE). Similar to LLE, the LMDS algorithm consists of two linear steps, the second of which solves an eigenvalue problem. The solution is globally minimized and does not suffer from the problem of local minima. Unlike LLE, however, LMDS produces locally isometric embedding results. The size of the eigenvalue problem scales with the number of patches rather than the number of data points. In addition, LMDS requires only local distances within each neighborhood as input.

(a) A Swiss-roll data set superimposed with local patches.

(b) 2D embedding by aligning the local patches.
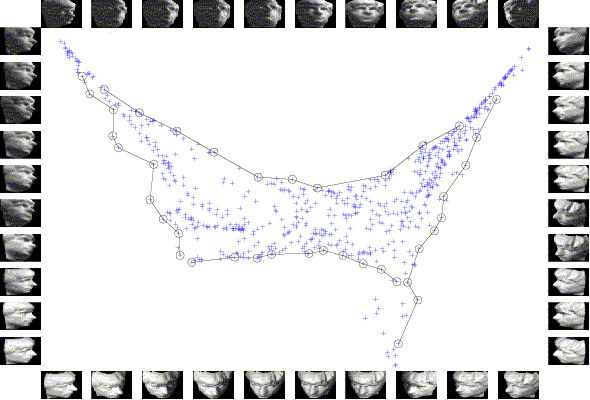
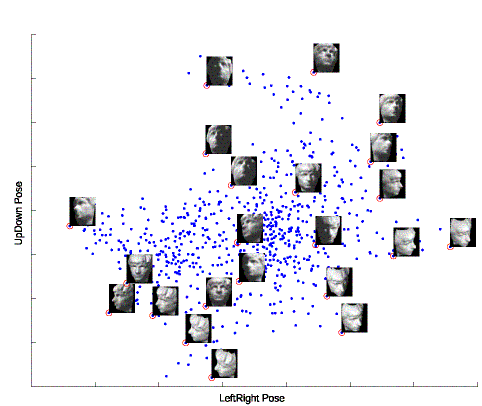
2D embedding of a data set of renderred face images, each shows a different pose of a human face. The data embedding is beset with sample images, where the data point representing each sample image is marked by a circle and all such points along each side of the embedding are connected in the same sequence as the images are listed along the side. We could observe strong correlations between the coordinates of these points and the horizontal and vertical poses and illuminations of the corresponding face images.
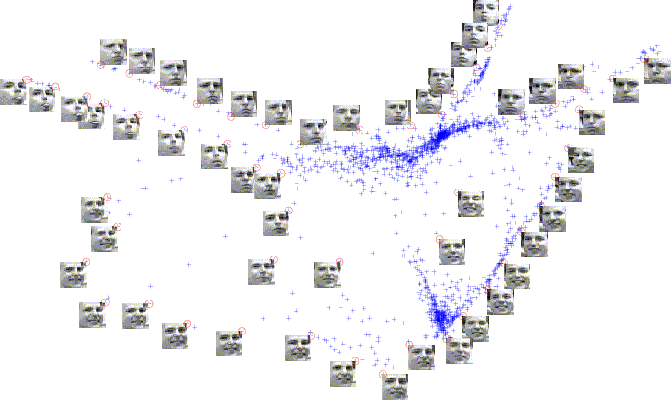
2D embedding of a video sequence data set inlaid with sample images, where a small circle located at a corner of each image marks the corresponding embedded data point representing the image. The embedded data points tend to form clusters, where images with similar facial expressions are grouped together or are arranged in sequence according to the strength of facial expressions.
We have also developed a non-parametric tetrahedral method of mapping data to 3D and have extended the method for projecting high dimensional data to arbitrary low spaces. The method projects data so that distances on a tetrahedron from each point to some of its near neighbors are exactly preserved. As shown below, data points are projected such that these tetrahedrons attach with each other. In the case that data points are distributed on a manifold, therefore, the method could unfold the swarm of data points. Intrinsic dimensionality is estimated by looking at the preservation of all distances as the dimensionality of the target space increases. This method does not require any user-specified parameter and works well when data are organized into clusters.

Projection of the renderred image data set using tetrahedral mapping.
Our current research in data embedding focuses on the development of robust and reliable embedding techniques, making these embedding techniques applicable to large relational data, making them work incrementally with growing data and data streams, and applications in multimedia information processing. In basic research, data embedding may benefit from ideas in differential geometry. It may play an instrumental role in extending theories of data and signal processing in Euclidean space to manifolds. These are the areas that we are interested in.
Updated: April 7, 2007 by Li Yang